blip.kummerlaender.eu

» Visualize the sky for arbitrary time and space coordinates on earth

The primary color of the sky is caused by Rayleigh and Mie scattering of light in the atmosphere. While attending the lecture on Mathematical Modelling and Simulation at KIT I implemented a ray marcher to visualize this. Together with a model for calculating the sun direction for given coordinates and times this allows for generating interesting plots:

For more details check out Firmament.

» Started working on a framework for generating LBM kernels

During the past exam season I now and then continued to play around with my GPU LBM code symlbm_playground. While I mostly focused on generating various real-time visualizations using e.g. volumetric ray marching, the underlying principle of generating OpenCL kernels from a symbolic description has not lost its promise.

This is why I have now started to extract the generator part of this past project into a more general framework. Currently boltzgen targets C++ and OpenCL using a shared symbolic description while providing various configuration options:

λ ~/p/d/boltzgen (boltzgen-env) ● ./boltzgen.py --help
usage: boltzgen.py [-h] --lattice LATTICE --layout LAYOUT --precision
                   PRECISION --geometry GEOMETRY --tau TAU [--disable-cse]
                   [--functions FUNCTIONS [FUNCTIONS ...]]
                   [--extras EXTRAS [EXTRAS ...]]
                   language

Generate LBM kernels in various languages using a symbolic description.

positional arguments:
  language              Target language (currently either "cl" or "cpp")

optional arguments:
  -h, --help            show this help message and exit
  --lattice LATTICE     Lattice type (D2Q9, D3Q7, D3Q19, D3Q27)
  --layout LAYOUT       Memory layout ("AOS" or "SOA")
  --precision PRECISION
                        Floating precision ("single" or "double")
  --geometry GEOMETRY   Size of the block geometry ("x:y(:z)")
  --tau TAU             BGK relaxation time
  --disable-cse         Disable common subexpression elimination
  --functions FUNCTIONS [FUNCTIONS ...]
                        Function templates to be generated
  --extras EXTRAS [EXTRAS ...]
                        Additional generator parameters

The goal is to build upon this foundation to provide an easy way to generate efficient code using a high level description of various collision models and boundary conditions. This should allow for easy comparision between various streaming patterns and memory layouts.

» Symbolically generate D3Q19 OpenCL kernel using SymPy

My recent experiments in using the SymPy CAS library for automatically deriving optimized LBM codes have now evolved to the point where a single generator produces both D2Q9 and D3Q19 OpenCL kernels.

Automatically deriving kernel implementations from the symbolic formulation of e.g. the BGK relaxation operator presents itself as a very powerful concept. This could potentially be developed to the point where a LBM specific code generator could produce highly optimized GPU programs tailored to arbitrary simulation problems.

» Experimental visualization of the velocity curl

Calculating the curl of our simulated velocity field requires an additional compute shader step. Handling of buffer and shader switching depending on the display mode is implemented rudimentarily for now. Most of this commit is scaffolding, the actual computation is more or less trivial:

const float dxvy = (getFluidVelocity(x+1,y).y - getFluidVelocity(x-1,y).y)
                 / (2*convLength);
const float dyvx = (getFluidVelocity(x,y+1).x - getFluidVelocity(x,y-1).x)
                 / (2*convLength);

setFluidExtra(x, y, dxvy - dyvx);

This implements the following discretization of the 2d curl operator:

Let $V : \mathbb{N}^2 \to \mathbb{R}^2$ be the simulated velocity field at discrete lattice points spaced by $\Delta x \in \mathbb{R}_{\gt 0}$. We want to approximate the $z$-component of the curl for visualization:

$\omega := \partial_x V_y - \partial_y V_x$

As we do not possess the actual function $V$ but only its values at a set of discrete points we approximate the two partial derivatives using a second order central difference scheme:

$\overline{\omega}(i,j) := \frac{V_y(i+1,j) - V_y(i-1,j)}{2 \Delta x} - \frac{V_x(i,j+1) - V_x(i,j-1)}{2 \Delta x}$

Note that the scene shader does some further rescaling of the curl to better fit the color palette. One issue that irks me is the emergence of some artefacts near boundaries as well as isolated “single-cell-vortices”. This might be caused by running the simulation too close to divergence but as I am currently mostly interested in building an interactive fluid playground it could be worth it to try running an additional smoothening shader pass to straighten things out.

» Add basic physical scaling and Knudsen quality criterion

The paper Automatic grid refinement criterion for lattice Boltzmann method by Lagrava et al. describes a criterion for measuring the local simulation quality using a comparison of the theoretical Knudsen number and the quotient of the cells’s non-equilibrium and equilibrium function.

While this criterion was developed to enable automatic selection of areas to be refined, it also offers a interesting and unique perspective on the fluid structure.

As the criterion requires calculation of the modeled Reynolds-, Mach- and Knudsen-numbers I took the time to set up the basics for scaling the simulation to actually model a physical system. Or rather calculating which physical model is represented by the chosen resolution and relaxation time.

» Published my BSc thesis on grid refined LBM in OpenLB

In addition to the PDF (German, ~60 pages) all sources including any referenced simulation data are available on Github and cgit. The resulting actual implementation of the grid refinement method by Lagrava et al. in OpenLB is currently not available publicly and likely wont make it into the next release. Nevertheless – if you are interested in the code and I have not yet found the time to release a rebased patch for the latest OpenLB release don’t hesitate to contact me.

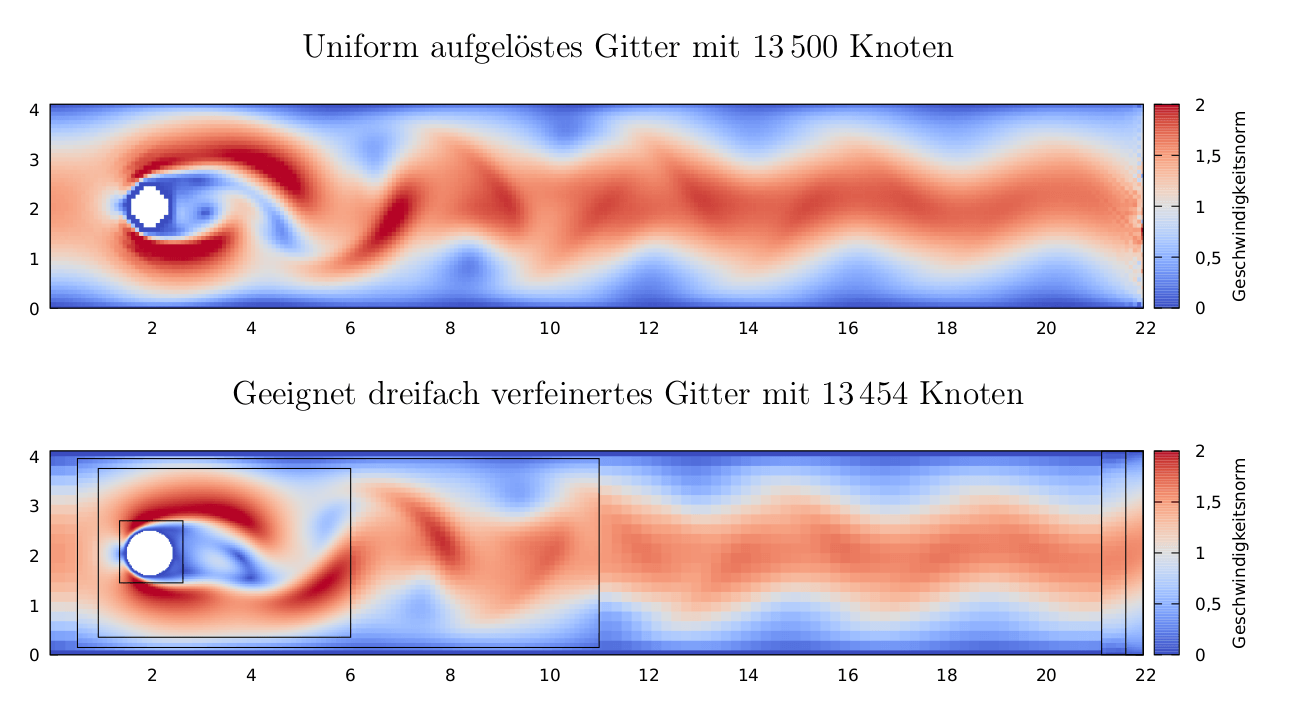
As a side note: The gnuplot-based setup for efficiently transforming Paraview CSV exports into plots such as the one above (i.e. plots that are neither misaligned Paraview screenshots nor overlarge PDF-reader-crashing PGFPlots figures) might be of interest even if one doesn’t care about grid refinement or Lattice Boltzmann Methods (which would be sad but to each their own :-)).